Autor: Raul Montoya Alarcon

Resolución de ecuaciones de 1º grado

Publicado el por Raul Montoya Alarcon

Ecuaciones de 1º grado

1.1.1 Ecuaciones tipo x+a=b ;  x-a=b

Primeras reglas

Si un término esta sumando a un lado de la ecuación pasa al otro lado restando. Si un término está restando a un lado de la ecuación pasa al otro lado sumando.

Si a la hora de despejar nos queda un –x tendremos que cambiarle el signo a ambos lados del igual, por ejemplo si –x=3 , cambiamos el signo a la –x y al 3 y quedará x=-3.

1.1.2 Como despejar una incógnita

Si un número está multiplicando pasa al otro lado dividiendo. Sí un número está dividiendo pasa al otro lado multiplicando.

Muy importante Error clásico

Si un número negativo está multiplicando pasa al otro lado dividiendo , pero sigue siendo negativo , NUNCA , PODEMOS CAMBIAR DOS OPERACIONES A LA VEZ , ( no pasa dividiendo-sumando).

1.1.3 Ecuaciones con varios términos con x 

Pasos:

Paso 1 Se transponen los términos Pasamos todas la x a la izquierda a los números a la derecha.

Paso 2 Operamos los términos.

Paso 3 Despejamos la x.

Las ecuaciones siempre si queremos se pueden comprobar, solo tenemos que sustituir la x por el valor que hemos obtenido.

EJERCICIOS:

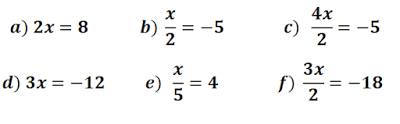
SOLUCIONES:

1.1.4 Ecuaciones de primer grado con paréntesis

Pasos:

Paso 1 Se eliminan los paréntesis.

Paso 2 Se transponen los términos Pasamos todas la x a la izquierda a los números a la derecha.

Paso 3 Operamos los términos.

Paso 4 Despejamos la x.

Ejemplo:

Primero eliminaremos los paréntesis exteriores. Empezamos por el de la izquierda. Este paréntesis tiene un signo negativo delante, por lo que cambiamos el signo a sus sumandos. Uno de los sumandos es otro paréntesis:

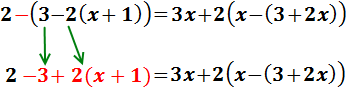
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Eliminamos el paréntesis que queda en la izquierda multiplicando por 2:

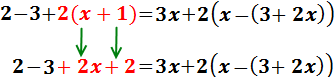
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Sumamos los números en el lado izquierdo para simplificar:

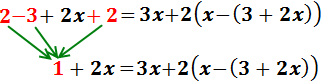
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Eliminamos el paréntesis exterior de la derecha multiplicando sus sumandos por 2:

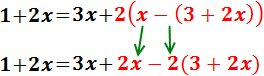
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Eliminamos el paréntesis que queda multiplicando por 2 y cambiando los signos:

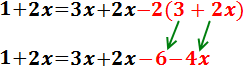
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Sumamos los monomios en el lado derecho:

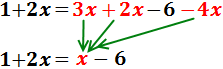
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Pasamos las x’s a la izquierda, los números a la derecha y simplificamos:

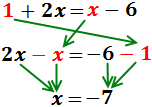
resolución de ecuaciones de primer grado paso a paso: ecuaciones simples, con fracciones, con paréntesis, con paréntesis dentro de otros, con signos negativos y ecuaciones sin soluciones o con infinitas soluciones

Por tanto, la solución es x = -7.

1.3.6 Ecuaciones de primer grado con paréntesis y denominadores

Pasos:

Paso 1 Quitamos paréntesis.

Paso 2 Hacemos el m.c.m.

Paso 3 Quitamos el m.c.m y Resolvemos.

Cuidado con los signos menos delante de una fracción porque afectan a TODOS los términos que hay en el numerador

EJEMPLO:


3x−43+2−3x2=1−x43x−43+2−3×2=1−x4

Como la ecuación tiene fracciones, multiplicamos por el mínimo común múltiplo de los denominadores (3, 2 y 4) para que desaparezcan.

Multiplicamos la ecuación por 12:

12⋅3x−43+12⋅2−3x2=12⋅1−x412⋅3x−43+12⋅2−3×2=12⋅1−x4

Simplificamos:

4(3x−4)+6(2−3x)=3(1−x)4(3x−4)+6(2−3x)=3(1−x)

Calculamos los productos:

12x−16+12−18x=3−3x12x−16+12−18x=3−3x

Resolvemos:

−6x−4=3−3x−6x−4=3−3x

−4−3=6x−3x−4−3=6x−3x

−7=3x−7=3x

El coeficiente 3 de la incógnita pasa dividiendo al otro lado:

x=−73x=−73

La fracción no puede simplificarse.

La solución de la ecuación es x=−73x=−73.